There’s a quote that’s often attributed to Albert Einstein which goes:
“If you can’t explain it simply, you don’t understand it well enough.”
Whether or not Einstein himself actually said this (it’s never been properly sourced, so it’s likely he didn’t), it’s still an insightful observation. It’s also one that yields a pretty powerful study tip when reversed:
If you want to understand something well, try to explain it simply.
By attempting to explain a concept in simple terms, you’ll quickly see where you have a good understanding of that concept. You’ll also be able to instantly pinpoint your problem areas, because they’ll be the areas where you either get stuck or where you end up resorting to using complex language and terminology.
This is the idea behind the Feynman Technique.
Named after the Nobel Prize-winning physicist Richard Feynman – who, in addition to being a brilliant scientist, was also called “The Great Explainer” for his ability to relay complex ideas to others in simple, intuitive ways – the Feynman Technique is a method for learning or reviewing a concept quickly by explaining it in plain, simple language.
In addition to helping you pinpoint those problem areas in the concept you’re trying to learn, the Feynman Technique gives you a quick, efficient way to shore up those areas using targeted learning. It’s a simple technique, but it’ll help you study much more efficiently once you put into action.
So how do you actually use it?
How to Use the Feynman Technique
Since the root of this technique involves explaining the concept, you could execute it in a number of ways – including literally grabbing a friend and explaining to them what you’re learning. However, you don’t always have willing friends at hand, so here’s the simpler method that just involves a sheet of paper.
- Step 1: Grab a sheet of paper and write the name of the concept at the top. You can use pretty much any concept or idea – even though the technique is named after Feynman, it’s not limited solely to math and science.
- Step 2: Explain the concept in your own words as if you were teaching it to someone else. Focus on using plain, simple language. Don’t limit your explanation to a simple definition or a broad overview; challenge yourself to work through an example or two as well to ensure you can put the concept into action.
- Step 3: Review your explanation and identify the areas where you didn’t know something or where you feel your explanation is shaky. Once you’ve pinpointed them, go back to the source material, your notes, or any examples you can find in order to shore up your understanding.
- Step 4: If there are any areas in your explanation where you’ve used lots of technical terms or complex language, challenge yourself to re-write these sections in simpler terms. Make sure your explanation could be understood by someone without the knowledge base you believe you already have.
That’s it!
3 Examples of the Feynman Technique in Action
As I mentioned earlier, simply defining a concept is only half the battle. If you want to explain is clearly, you have to apply it by working through examples.
In the spirit of eating my own dog food, I’ve included three examples of how you might use the Feynman Technique below.
Example #1: The Pythagorean Theorem
We’ll start with a very simple example. The Pythagorean Theorem shows how you can find the length of any right triangle’s hypotenuse:

When I initially started writing this explanation, I simply wrote the sentence at the top and then added the formula.
However, note how the final page has a couple of additions:
- A small picture showing what a right triangle is
- An arrow clarifying the nature of C in the formula
This was my attempt to go back and further simplify the explanation. Even with a basic mathematical theorem like this one, there are still assumptions and terms that encompass ideas that you may not be 100% clear on. Challenge yourself to identify those things and define them.
Example #2: Bayes’ Theorem
Since the Pythagorean Theorem is a pretty simple concept, I thought you might like to see an example using something more complex. Bayes’ Theorem – a concept used in probability theory and statistics – fit the bill nicely.

And here’s a page working through a specific example and using the formula:

These pages do a decent job of explaining Bayes’ Theorem at a very broad level, but I’ll be the first to admit that this is a topic that takes a good long while to truly grasp.
In fact, I had to spend three hours reading through A.I. researcher Eliezer Yudkowsky’s 15,000-word explanation of the theorem before it “clicked” in my brain, so definitely check that article out if you’re curious. You can also check out Arbital’s more recent guide, which is – by Yudkowsky’s own admission – much better and easier to follow.
Example #3: The CSS Box Model
Here’s an example of how the Feynman Technique can be used to review a non-mathematical concept.
The CSS Box Model is a tool for representing the size of HTML elements (i.e. the code that makes up web pages just like the one you’re reading right now), as well as the spacing around them. I chose it as an example because it’s a concept that took me a long time to grasp back when I started learning how to build websites as a teenager.

To clarify that page’s general explanation, here’s an example of an element with specific height, width, margin, padding, and border values written in CSS code:
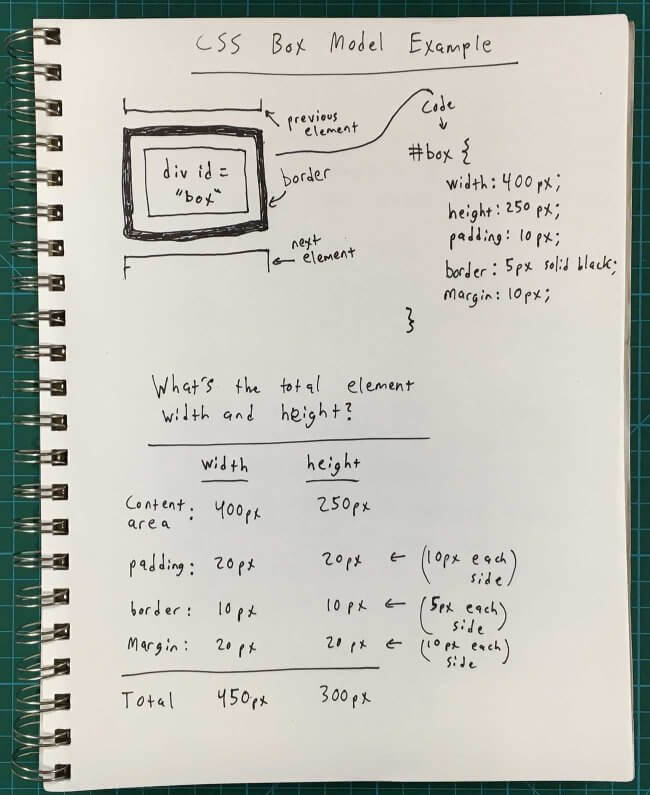
In addition to writing the code out, I thought it would be extra helpful to show exactly how each attribute affects the overall size of the element.
To a budding web developer, it might not be immediately obvious that, say, a padding value of 10px actually increases the element’s width by 20px overall (because the 10px is applied to each side).
If you happen to be curious about the Box Model and want to learn more, check out this guide.
Go Further: The LPC Method
If you want to make the Feynman Technique even more effectively, you can pair it with a study technique I call the LPC Method – which stands for Learn, Present, Critique.
As with the original Feynman Technique, the goal is to deepen your understanding of a concept by explaining it – but in this instance, you present to a camera and then critique your performance later on.
To learn more about how to use this method, watch the video above or check out my in-depth guide to the the LPC Method on my personal site.
Think Like a Child
One final tip: While you’re working through the Feynman Technique for any given concept, it can be useful to pretend that you’re explaining that concept to a child.
Doing this will boost your own understanding for one simple reason; in addition asking things like, “Can I have another Oreo?” and “Can I go watch Dragon Ball Z now please?” a kid is probably going ask…
“Why?”
While older people often become accustomed to taking things at face value, kids are naturally curious. They’re quick to point out their confusion.
If you teach a kid how the Pythagorean Theorem works and give him the formula for using it, there’s a good chance he’ll ask you:
“Why does that formula work? How can you know it’ll always work? Prove it, sucka!”
…and then you realize that the kid was actually Mr. T in disguise all along, and now your life depends on being able to explain a geometry concept. How did you even get here?
Seriously, though, this is a great mindset to adopt. Maybe you do know how the Pythagorean Theorem works, and maybe you can easily draw out the proof by rearrangement:
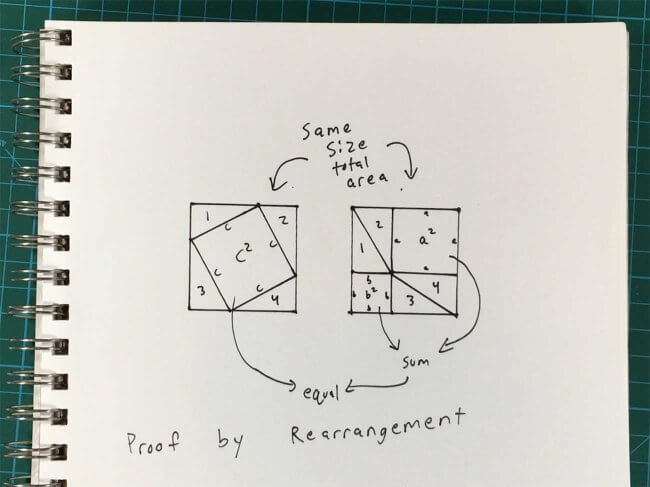
When it comes to other concepts, though, it’s likely that you’re relying on assumptions, heuristics, and other black boxes when it comes to certain details. So adopt a child-like mindset and challenge yourself to clearly explain the whole concept.
Once you’ve done that and worked through all the steps, you can further refine your knowledge of whatever you’re studying with other techniques, including:
Hope this helps!
If you’re unable to see the video above, you can view it on YouTube.
Looking for More Study Tips?

If you enjoyed this article, you’ll also enjoy my free 100+ page book called 10 Steps to Earning Awesome Grades (While Studying Less).
The book covers topics like:
- Defeating procrastination
- Getting more out of your classes
- Taking great notes
- Reading your textbooks more efficiently
…and several more. It also has a lot of recommendations for tools and other resources that can make your studying easier.
If you’d like a free copy of the book, let me know where I should send it:
I’ll also keep you updated about new posts and videos that come out on this blog (they’ll be just as good as this one or better) 🙂
Video Notes
- Scott Young’s video – where I originally heard about this technique
- The Feynman Notebook Method – related concept on Cal Newport’s blog
- Surely You’re Joking, Mr. Feynman! – a book of stories about Richard Feynman’s life, written by Feynman himself. I read this book last year and loved it.
Have something to say? Discuss this episode in the community!
If you liked this video, subscribe on YouTube to stay updated and get notified when new ones are out!


