Despite all of the research that shows mathematicians are made and not born, I don’t blame you for thinking you’re simply bad at math, because math is friggin’ hard.
To build your math “house” you have to make sure each knowledge chunk fits perfectly so you can build on top of it without the fear that it’ll all topple over later.
And if you slack on just one fundamental topic, your knowledge will collapse in the face of teeth-grinding all-nighters over problem sets and a palpitating heart on the big exam.
So the money question is this: How do you get better at math?
To get better at math, you need to master progressively harder math problems by employing a strategy psychologist Anders Ericsson calls deliberate practice in his book Peak: Secrets from the New Science of Expertise.
He defines it as “purposeful practice that knows where it is going and how to get there.”
This means that you have to intentionally find problems that stump you and work through them. And if the problem is too hard, find an easier one to solve first.
This is one of the most important first principles you need to keep in mind when learning math. In this post, I’ll be sharing some tips on how you can do just that.
Tip #1: Break Down Complex Problems Into Simpler Ones
“If you can’t solve a problem, then there is an easier problem you can solve: find it.”
— George Pólya, How to Solve It
To get at the meat of each problem, you have to identify the concepts, isolate them, and practice. Let’s take this summation problem, for example:
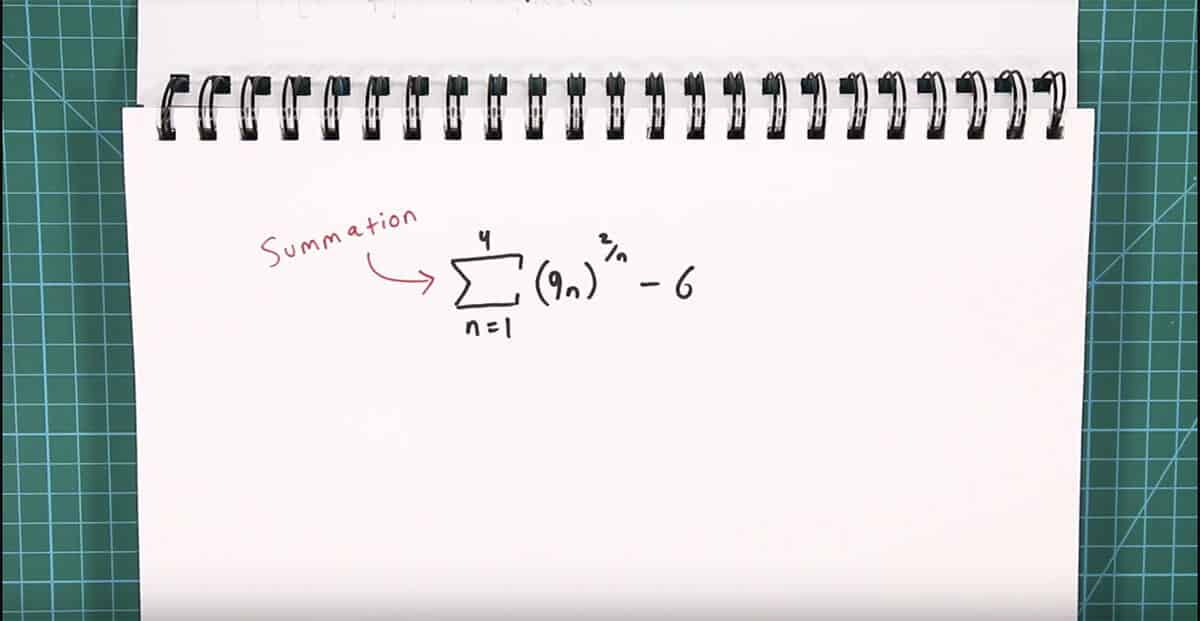
It’s a relatively simple problem that a senior high school student should be able to do. But there’s a part of the equation that makes things complicated:
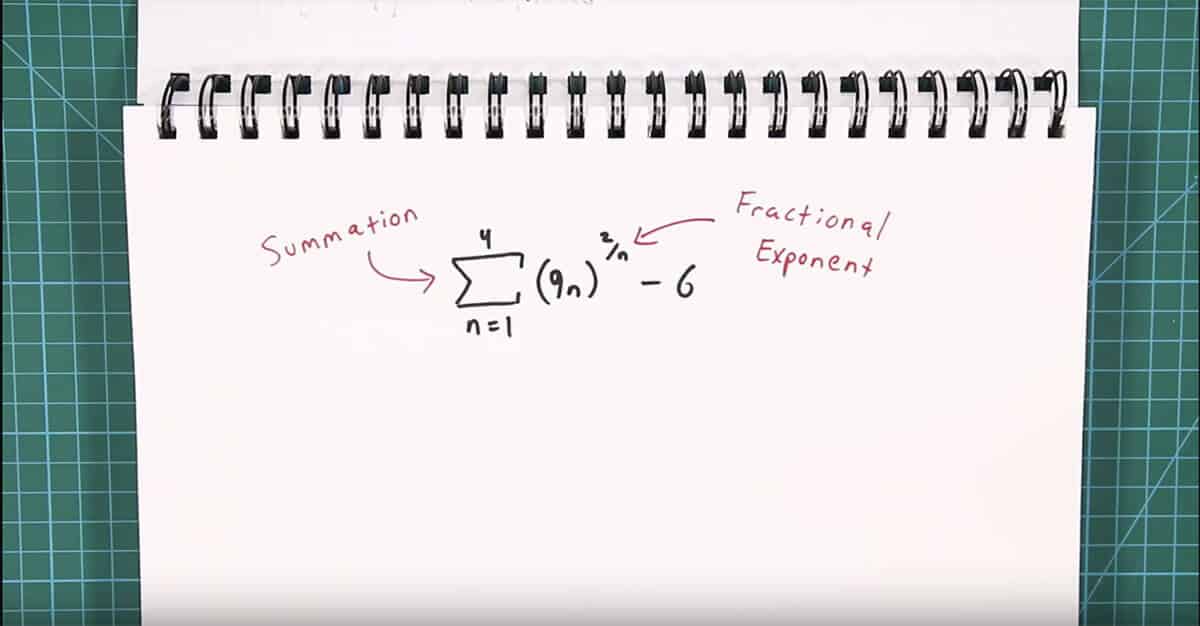
The problem requires that you have a knowledge of summation and fractional exponents to solve it.
So before you dive into the problem, you have to make sure you understand summation and fractional exponents on their own first.
For example, you could take out the fractional exponent and work through the initial problem without it:
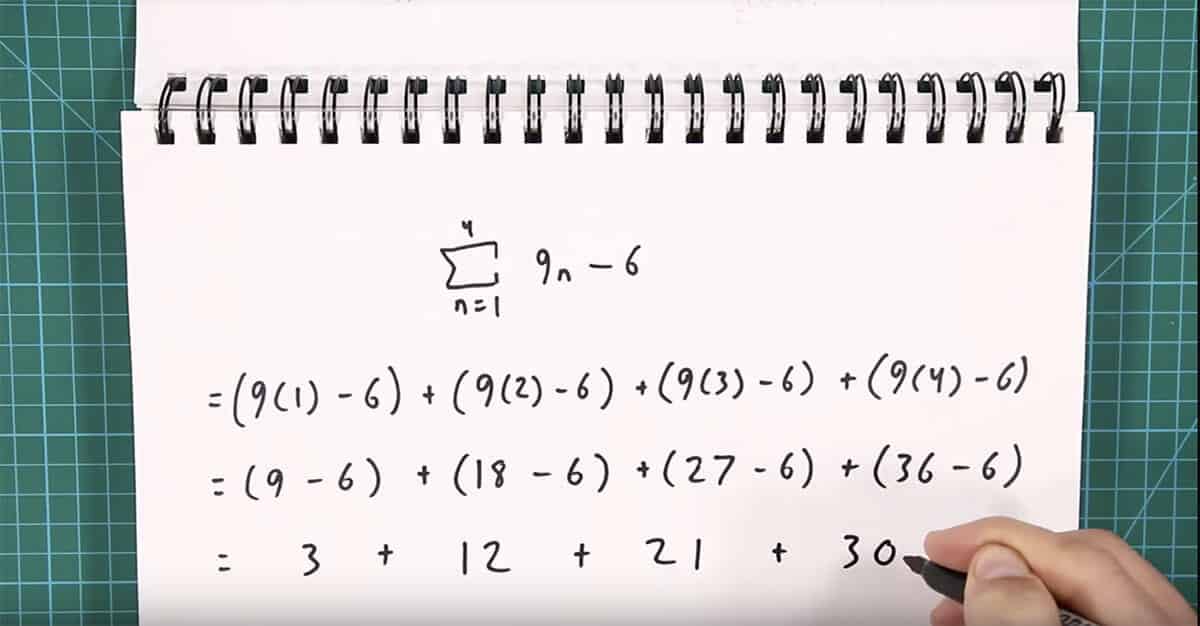
Which then gets you the following solution:

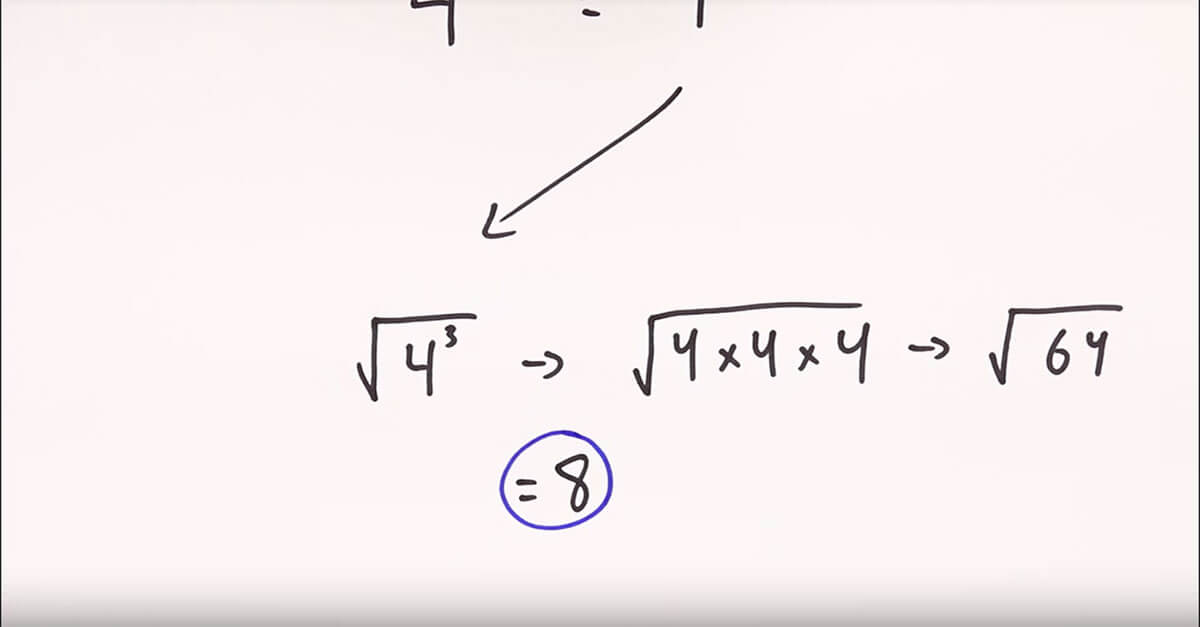
Next, you could take out the fractional exponent in the problem and work on mastering that:
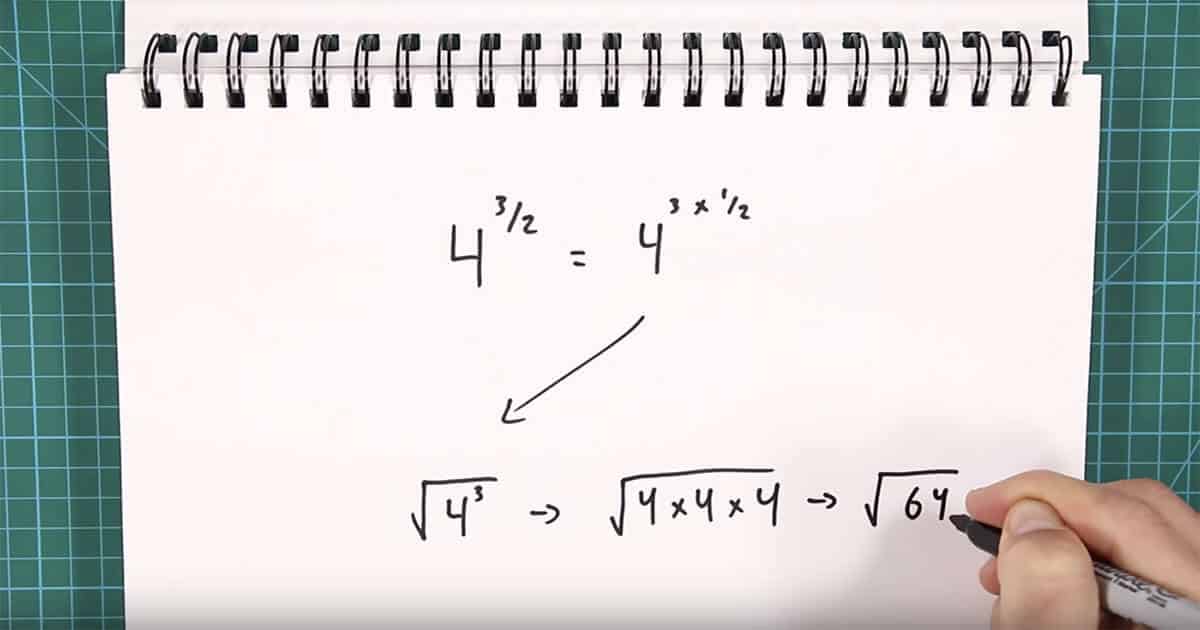
And realize that it’s not that complicated to solve by itself:
Once you’ve figured out those two concepts on their own, then you can put them together to solve the initial equation. Check out how they all go together:
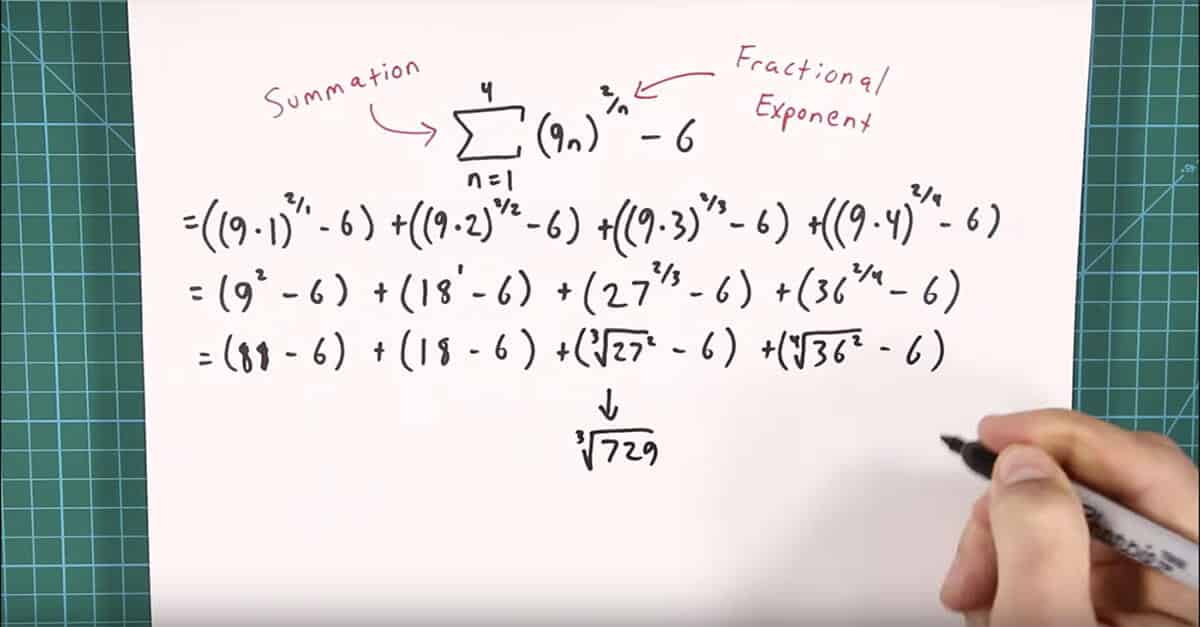
Congrats! You’ve now found the solution:
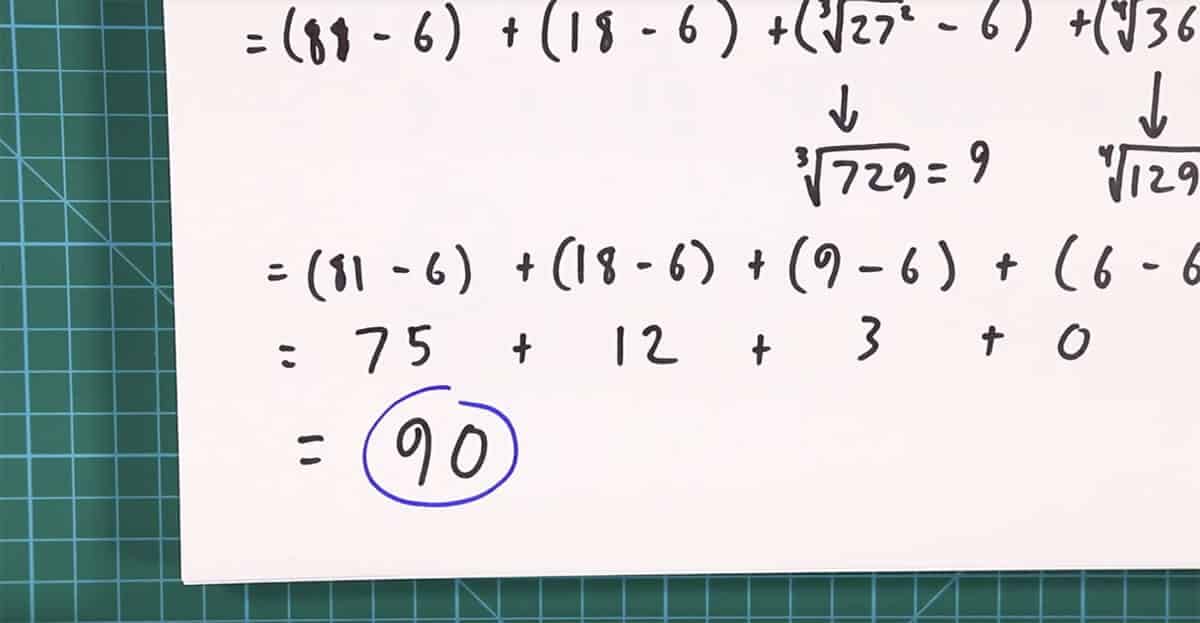
Tip # 2: Use Simple Numbers
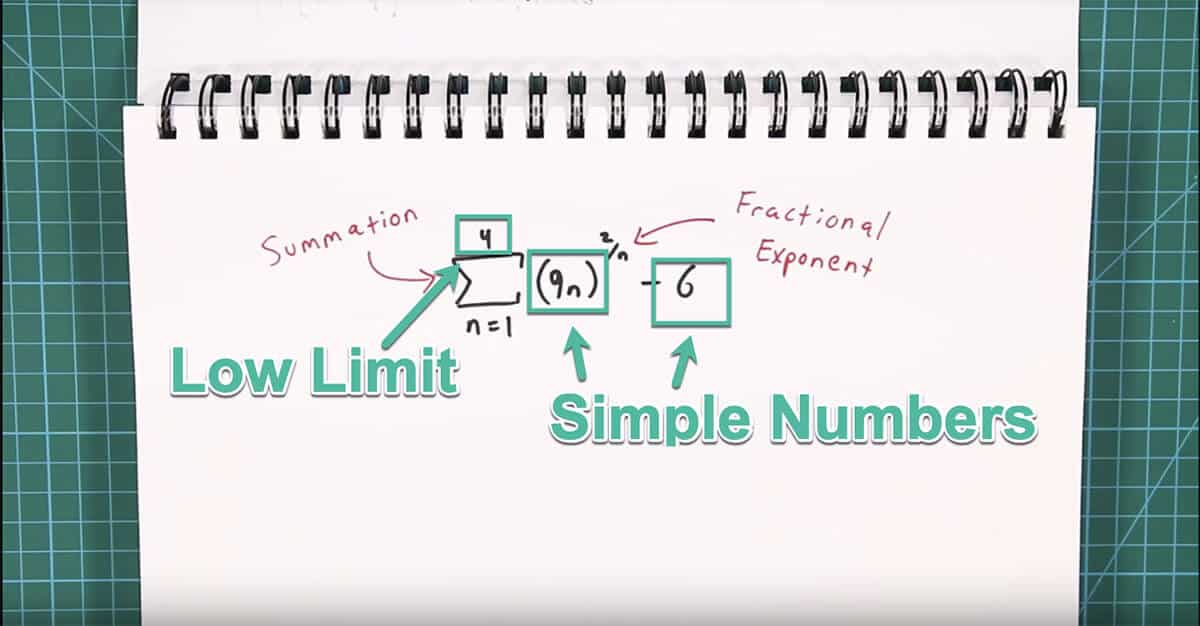
If you take a look at my example again, you’ll notice that it uses simple numbers and a low limit:
- The simple numbers mean I don’t need a calculator to do the operations
- The low limit means that I won’t tire my brain out with a repetitive operation that I already know how to do
Similarly, when you study, work on problems that have simple numbers first. Instead of the complexity of the problem, working with problems that have small, whole numbers let you zero in on the concepts and principles.
Tip #3: Review the Underlying Concepts
Sometimes though, your understanding is just too shaky for the problem. (OK, let’s be honest: this is most of the time.)
In that case, it’s time to dig into your book and look through your notes from class. (I’m assuming you take A+ notes. If not, learn how to take better notes here.)
If you still don’t get it, there are lots of YouTube videos and explainer articles to help you. Oftentimes, these have step-by-step solutions that show how other people get to their answers:

Finally, ask your professor or teacher for help. Ericsson says, “A good math teacher… Will look at more than the answer to a problem; he’ll look at exactly how the student got the answer as a way of understanding the mental representations the student was using. If needed, he’ll offer advice on how to think more effectively about the problem.”
Skilled teachers can often reword or re-frame concepts. Sometimes, all it takes is a slightly different word choice for a tricky concept to click into place.
Tip #4: Get Step-by-Step Instructions from an Online Tool
Sometimes it’s helpful to see a step-by-step solution to a problem you’re working on, as long as you try to figure it out for yourself first.
There are three great tools to get solutions to problems you’re struggling with:
Wolfram Alpha is a tool that can solve basically any math problem, as well as give you detailed solutions (though you’ll need the premium version to see all the steps):

In contrast, although Symbolab’s user interface is clunkier and less intuitive, its step-by-step solutions are free:
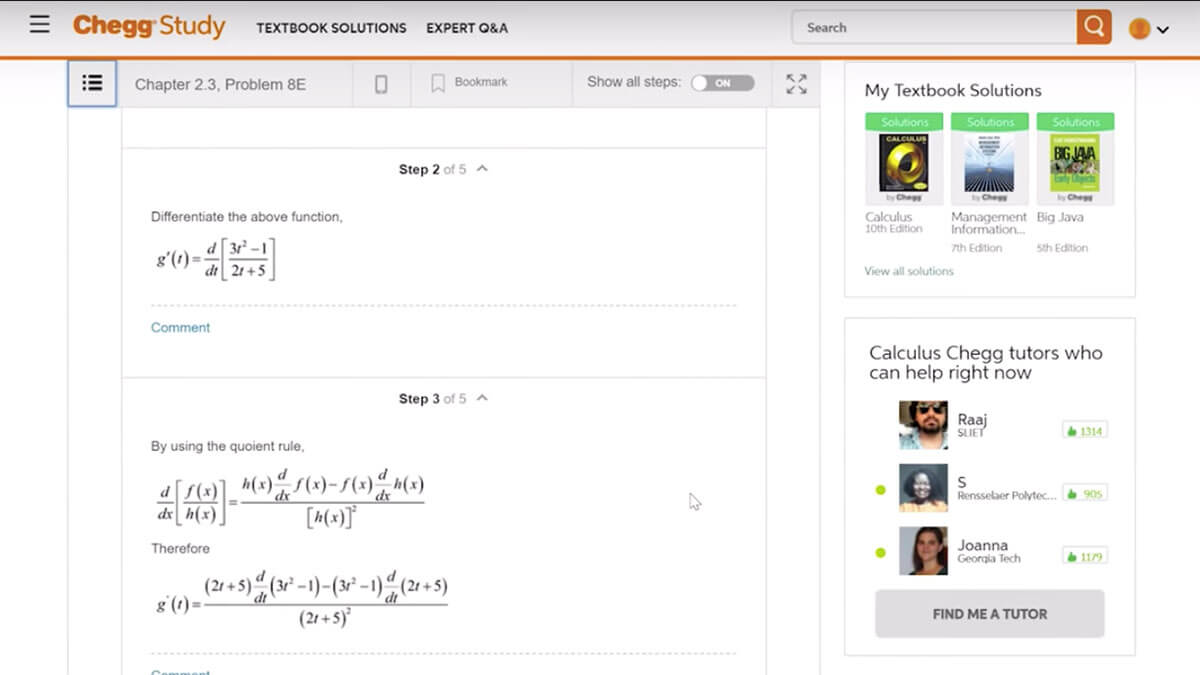
Finally, if you need solutions to specific problems in your textbook, you can check out Chegg Study. It will show you step-by-step solutions for all problems in the textbook your math class uses:
Regardless of what you choose, make sure you try the problems out yourself afterwards without looking at the solutions.
This helps you avoid what Jeffrey Karpick, a researcher specializing in learning strategies for students, calls an illusion of competence. This is when you feel like you understand a concept because you’ve read a paragraph multiple times and can process it faster
Instead of rereading, Karpick found that attempting to retrieve information from memory is the most effective form of studying. He advocated for methods like the Feynman Technique to help you recall and remember concepts deeply.
Likewise, ask yourself honestly: Have I pushed my brain to its limit trying to solve this problem first? If you have but you still can’t get it, it’s fine to look up the answer. But after that, challenge yourself to go back and work through the problem without looking at your notes and references.
Again, the whole point of math is to master the concepts you’re working with so you can build on top of them, not just to get through the homework.
Tip #5: Don’t Rush Your Homework
“Just understanding how a problem was solved does not necessarily create a chunk that you can easily call to mind later. Do not confuse the “aha!” of a breakthrough in understanding with solid expertise!”
– Barbara Oakley
It’s very tempting to work through homework problems as fast as you can so you can get back to playing Civilization VI or The Witcher 3.
But technical subjects like math and science require that you take things slow.
For starters, in engineering professor Barbara Oakley’s book A Mind for Numbers, Oakley suggests applying spaced repetition. Instead of spending long hours in the library, she advises shorter, more frequent study sessions that are spread out over weeks, not days.
This kind of slow, deliberate learning allows your brain to get a firm grasp of each concept and more importantly, the connections between them.
To truly be a master of your tools, you need to learn how to adapt them to different situations.
Similarly, to truly say that you’ve mastered a chunk of math, you need to see through the problems and know which formula or process to use in a heartbeat.
Learning Math Can Be Satisfying
“I don’t believe in the idea that there are a few peculiar people capable of understanding math, and the rest of the world is normal. Math is a human discovery, and it’s no more complicated than humans can understand.”
– Richard Feynman, Omni Magazine
Getting better at math is simple but not easy.
You need to deeply understand both how a concept works and when to use it alongside other concepts and operations.
To help you gain mastery in the individual mathematical building blocks, you can use references and tools to help you. But ultimately, they can only help you so far.
To gain mastery of the underlying concepts you have to get your pencil and paper and solve the hard problems yourself.

